Analyzing free classification results: Multi-dimensional scaling (MDS) analyses

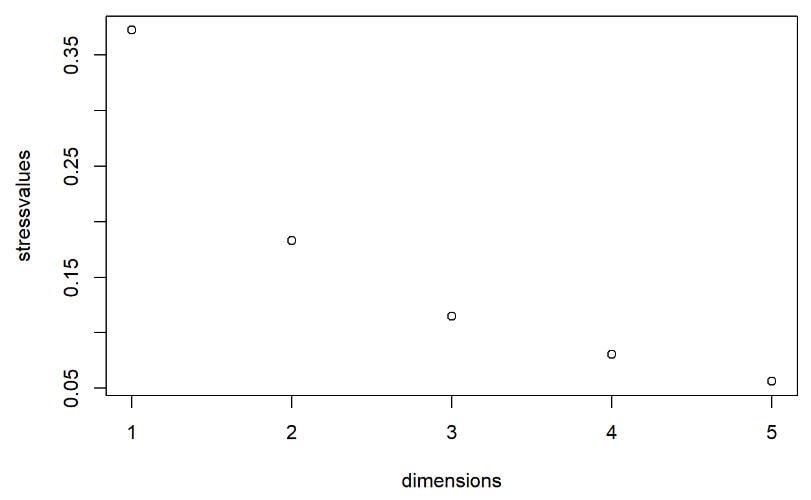
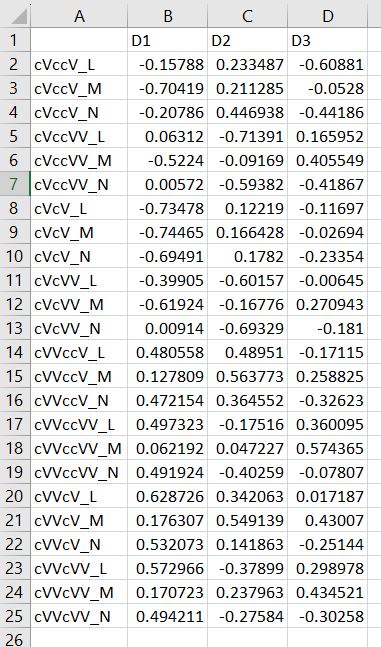
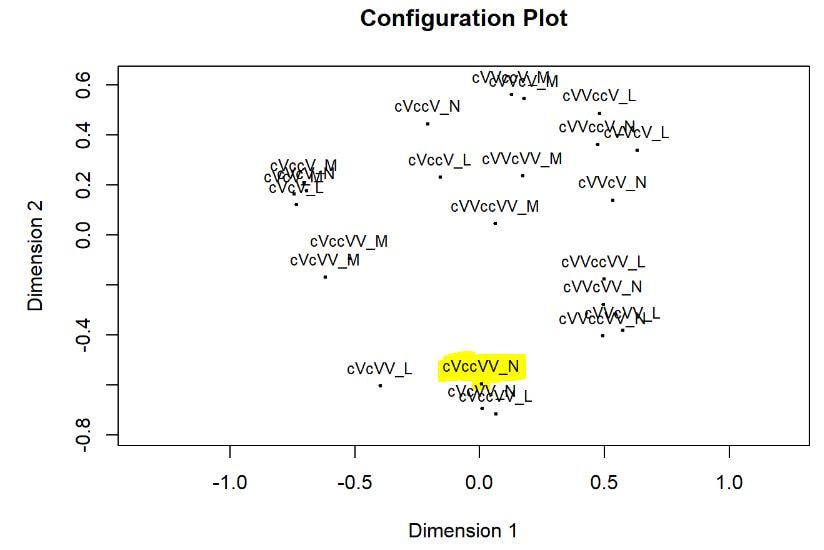
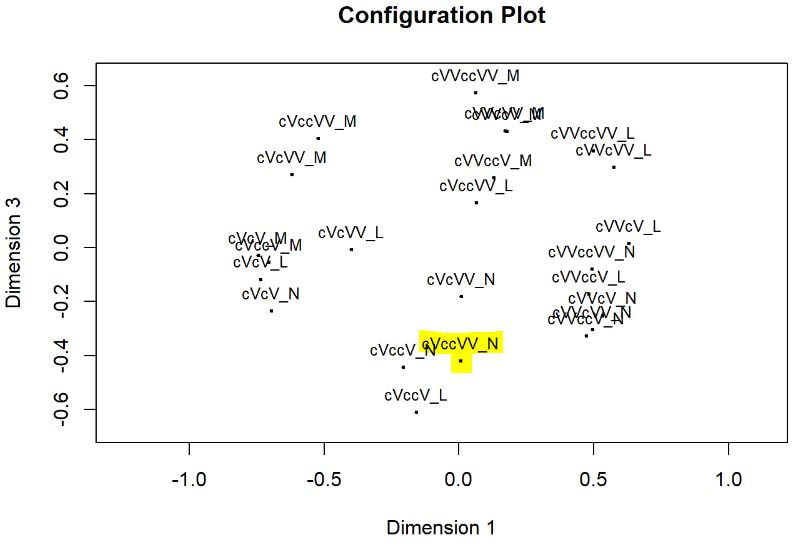
Multi-dimensional scaling (MDS) is a way of determining the placement of each stimulus in space so that the perceptual distances between the stimuli are recreated as closely as possible, with stimuli that were judged to be more similar placed closer together and stimuli judged to be less similar placed further apart.  If you're not familiar with MDS, you may find the explanation on pp. 1107-1108 of our 2023 SSLA article on free classification to be useful. 

You can perform MDS analyses on any of the matrix outputs from the create_FC_similarity_matrices.Rmd file from the previous blog post using this R Markdown file.  A pdf example using this script to analyze our Finnish length data can be viewed here.

In order to decide the appropriate number of dimensions for your data, it's a trade-off between minimizing model misfit (stress) and maximizing the amount of variation explained (R-squared, "R2"), as well the interpretability of the solution.  As we say in our SSLA article (pp. 1112-1113):

Because higher stress in MDS indicates greater model misfit, Clopper (2008, p. 578) recommends looking for the “elbow” in the stress plot to find the number of dimensions beyond which stress does not considerably decrease, whereas Fox et al. (1995, p. 2544) recommend looking for the number of dimensions beyond which  does not considerably increase, provided that this number of dimensions is interpretable based on the relevant theory. Clopper (2008) also states that a stress value of less than 0.1 for the matrix is considered evidence of “good fit,” although she acknowledges that this is rarely achieved in speech perception data. ​

Unfortunately the R package for MDS that I used in the R Markdown file doesn't give R2 values (if this is important, you can obtain these with an MDS analysis in SPSS); however, we can look at the stress amounts and the plot produced by the script.  In the stress plot for our Finnish length data, there is no clear elbow in the plot, but rather a gradual decrease in model misfit.  We decided on a 3D solution, but a 2D solution would also be appropriate.  A 1D solution has clearly too much stress, while a 4D or 5D solution would be very difficult to interpret and visualize.

This script will save text files of the dimension scores for 1, 2, 3, 4, and 5 dimensional solutions.  The dimension scores are the points in space of each stimulus. In the image below, we see the 3 dimensional solution of our Finnish length data, combined across contexts.  You can think of D1, D2, and D3 as (x, y, z) coordinates.  For example, in row 7, we see that the average CVCCVV token for speaker N (averaged across pata, tiki, and kupu contexts) is placed by the MDS solution at x = 0.00527, y = -0.59382, z = -0.41867.  

When Dimension 1 x Dimension 2 (i.e. x and y coordinates) and Dimension 1 x Dimension 3 (i.e. x and z coordinates) are plotted , we see where CVCCVV_N is placed relative to other stimuli.  You can think of the second graph (Dim1 x Dim3) as viewing the first graph from above. 

In these plots, you can somewhat see that the stimuli are grouping together mainly by vowel length rather than consonant length (e.g. Dim 1 has mostly short V1 on the left and long V1 on the right), but it's still difficult to interpret.  For this reason, we recommend rotating the solution (i.e. moving all of the points in a certain way by a specific amount) to provide a better visualization.  This doesn't change the position of the points relative to each other, which is the important part in an MDS solution.  My colleague Ryan Lidster did this in Excel, but since that was rather clunky, I'm working with him on creating an R script to aid in rotating MDS solutions and plotting them.  Stay tuned!